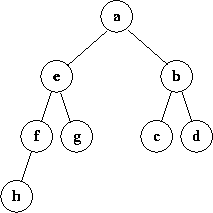
- Preorder:
a, e, f, h, g, b, c, d - Inorder:
h, f, e, g, a, c, b, d
Answer:
- Write a method that overloads
operator==to determine whether two trees are equivalent, using an enumerator and without recursion. What is the time complexity?Answer (based on the solution of Zhengtao Cui):
template <class Object> bool BinaryTree<Object>::operator== (BinaryTree<Object>& bt) { // BinaryTree<Object>::operator== if (isEmpty()) return bt.isEmpty(); return (*(root()) == *(bt.root())) && (*(left()) == *(bt.left())) && (*(right()) == *(bt.right())); } // BinaryTree<Object>::operator==Time complexity: O(n), because it recursively visits each node of each tree exactly once.
- Write a method that overloads
operator==to determine whether two trees are equivalent, not using an enumerator and with recursion. What is the time complexity?Answer (based on the solution of Gwendolin Ting):
template <class Object> bool BinaryTree<Object>::operator== (BinaryTree<Object>* bt) { // BinaryTree<Object>::operator== Enumeration<Object>* e = inOrderEnumerator(); Enumeration<Object>* ee = bt->inOrderEnumerator(); bool returnValue = true; while (returnValue && (e->hasMoreElements() && ee->hasMoreElements())) returnValue = returnValue && (ee->nextElement() == ee->nextElement()); if (e->hasMoreElements() || ee->hasMoreElements())) returnValue = false; delete e; delete ee; return returnValue; } // BinaryTree<Object>::operator==Time complexity: O(n), because it visits each node of each tree exactly once, via their enumerators.
Ask for help with this question.
A of size n.
A
globally balanced binary search tree
has
A[mid]
in the root of the tree,
the left subtree is the
globally balanced binary search tree
of the elements in the subarray
A[0..mid-1],
and
the right subtree is the
globally balanced binary search tree
of the elements in the subarray
A[mid+1..n-1].
Write a method to construct a
globally balanced binary search tree
from a sorted array A.
What is the time complexity?
Answer (based on the solution of Faron Fullbright):
template <class Object>
BinarySearchTree<Object>& BinarySearchTree<Object>::join (
BinarySearchTree<Object>& T1,
Object& x,
BinarySearchTree<Object>& T2)
{ // BinarySearchTree<Object>::join
Enumeration<Object>* T1e = T1.preOrderEnumerator();
Enumeration<Object>* T2e = T2.preOrderEnumerator();
BinarySearchTree<Object>* newTree =
new BinarySearchTree<Object>;
newTree->insert(x);
while (T1e->hasMoreElements())
newTree->insert(T1e->nextElement());
while (T2e->hasMoreElements())
newTree->insert(T2e->nextElement());
if (T1e != NULL) { delete T1e; T1e = NULL; }
if (T2e != NULL) { delete T2e; T2e = NULL; }
return *newTree;
} // BinarySearchTree<Object>::join
Time complexity: O(n), because it visits each node of each tree exactly once, via their enumerators.
Ask for help with this question.
T1
and
T2
be two binary search trees such that
every element of
T1
is less than
every element of
T2.
Let
x
be a value such that
T1
<
x
<
T2.
Write a method
join(T1,x,T2)
that produces a binary search tree
containing the elements of
T1,
x
and
T2.
Note that no node of the result of
join
should point to any node of
T1
or
T2;
i.e., the method must copy every node of each tree.
What is the time complexity of
join?
Answer (based on the solution of Adam Heck):
template <class Object>
BinarySearchTree<Object>* BinarySearchTree<Object>::makeTree (
ArrayClass<Object>& a, int start, int end)
{ // BinarySearchTree<Object>::makeTree
BinarySearchTree<Object>* bst;
int mid = (start + end) / 2;
if (end < start) return new BinarySearchTree<Object>;
bst = new BinarySearchTree<Object>(a[mid]);
bst->_left = makeTree(a, start, mid - 1);
bst->_right = makeTree(a, mid + 1, end);
return bst;
} // BinarySearchTree<Object>::makeTree
Time complexity: O(n), because it visits each value of the array exactly once, and its recursive calls build the immediate children of the calling node.
Ask for help with this question.