HAMR

Hierarchical Adaptive Mesh Refinement

Welcome to Henry Neeman's HAMR page!

Download my thesis, Autonomous Hierarchical Adaptive Mesh Refinement for Multiscale Simulations, in PostScript or PDF format. Warning! My thesis is about 11Mb of PostScript, including two full color renderings.

As part of my dissertation, I developed HAMR, the Hierarchical Adaptive Mesh Refinement system, which is an autonomous, general-purpose adaptive mesh refinement system for multiscale structured simulations that implements the AMR strategy of Marsha Berger -- now a professor of computer science at the Courant Institute of Mathematical Sciences at New York University -- and various collaborators.

You can learn more about AMR by visiting Tomek Plewa's excellent AMR page, which has links to many major AMR researchers.

PREVIOUS WORK

I worked on a simulation of the impact of Comet Shoemaker-Levy 9 on Jupiter, which happened back in 1994. I collaborated with Mordecai-Mark Mac Low of the American Museum of Natural History; Greg Bryan of the LCA (and my officemate), who provided the physics solver CMHOG, which uses the piecewise parabolic method (PPM) to solve the equation of gas dynamics, as well as other software and physics support and information; Mike Norman; and various other collaborators. We managed to run 100 timesteps (about 45 seconds of physical time) of this simulation, which showed us some bugs we weren't aware of.

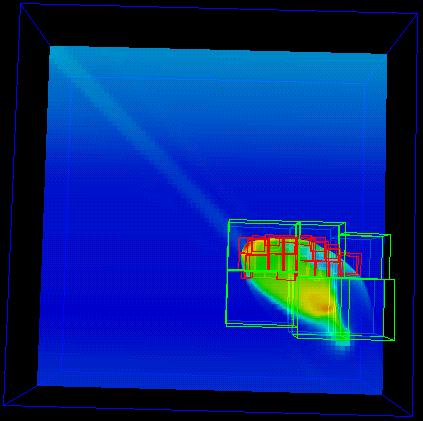
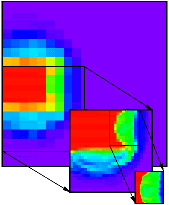
Here's a look at a recent run; the images are from roughly 35.3 seconds simulated physical time after impacting Jupiter's inner atmosphere.

image of comet specific energy

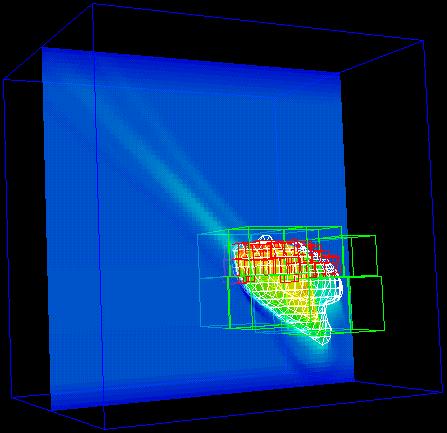
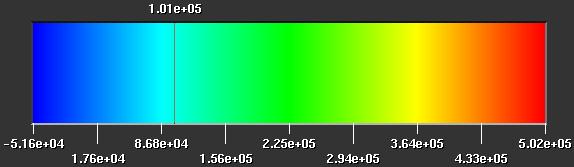
image of comet z-velocity image of comet z-velocity colorbar

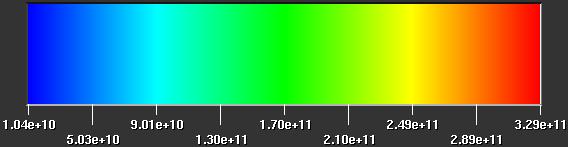
The front facing view is of specific energy, which is roughly analogous to temperature. The diagonal view with the wireframe isosurface is vertical velocity. The isovalue of the surface is expressed in centimeters per second, so it shows where the vertical velocity is about 101 km/sec, which is over 200,000 miles per hour. Colorbars are included as a reference.

The blue outer box represents the coarsest grid, which is 72 x 60 x 72 cells covering a region of physical space 648 x 540 x 648 kilometers; each cell is 9 x 9 x 9 km. The green boxes represent the intermediate level grids, which have a resolution of 3 x 3 x 3 km per cell. The red boxes represent the finest level grids, which have a resolution of 1 x 1 x 1 km per cell.

Performance on this run was pretty good, but we know the next run will be even better. This particular experiment, running on an SGI Power Challenge supercomputer, ran for 97 timesteps, took about four and half days of real life and used 187.5 CPU hours; the expected time on a uniform grid of the finest resolution would be 5498.6 CPU hours, so the speedup was a factor of 29.3. Memory use was about a gigabyte (one billion bytes), compared to an expected 10.4 Gb on a uniform finest grid.

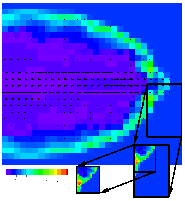
Here's another experiment, showing a cosmic jet. Details to come.

thumbnail image of cosmic jet specific energy Click on the thumbnail image to get the full-size image.

thumbnail image of cosmic jet density with velocity arrows Click on the thumbnail image to get the full-size image.

Another slice of the 3D cosmic jet experiment. The root level domain is 99 x 30 x 30 zones covering 33 x 10 x 10 core radii. The refinement factor between each pair of adjacent levels is 3, so the effective resolution is 891 x 270 x 270. This image shows the jet after 1.64 sec simulated physical time (270 timesteps), depicting 0 < x < 10, -4.6667 < y < +4.6667, z approximately 0. The quantity shown is density, with u-v velocity arrows overlayed. The simulation took 23.2 CPU hours on 8 processors of an SGI Power Challenge, with a speedup factor of slightly under 6 compared to running serially. The speedup over a single, uniform grid of finest resolution is about a factor of 180.

Dave Nelms' HAMR page (Hand Actuated Mental Reconditioning). It has nothing to do with Hierarchical Adaptive Mesh Refinement, but Dave tells me he like echidnas too, so what the heck.

Maintained by Henry Neeman
(hneeman@ou.edu)

URL: http://hneeman.oscer.ou.edu/hamr.html